Книга «Как измерить все, что угодно». Этот материал — это субъективная попытка создателей и участников проекта «Читай Быстро» выделить главное из книги Дугласа Хаббарда «Как измерить все, что угодно. Оценка стоимости нематериального в бизнесе». Читайте краткое содержание — принимайте решение, стоит ли читать всю книгу целиком.
| Название: | Как измерить все что угодно |
|---|---|
| Автор книги: | |
| Жанр: | Бизнес |
| Издательство: | Олимп-Бизнес |
| Год издания: | 2009 |
| ISBN: | 978-5-9693-0163-4 |
| Рейтинг: |
Содержание
Измерение: решение существует
«Вопросы Ферми»
Четыре предпосылки измерения
Универсальный подход к измерению чего бы то ни было.
Прежде чем приступить к измерениям
Формулирование задачи по измерению
Неопределенность и риск
Методы повышения качества калибровки вероятности
Оценка стоимости информации
Стоимость информации для переменных величин
«Уравнение прозрения»: стоимость информации меняет все
Методы измерения
Калькуляторы
Правило пяти
Метод Монте-Карло
Пояснения Монте-Карло
Идеи из книги
Переход от объекта к способу измерения
Инструменты наблюдения: введение в инструментарий измерения
Разложение на составляющие: алгоритм
Вторичные исследования: предположим что до вас этот объект уже измеряли
Учитывайте погрешность
Как наблюдение за частью рассказывает нам о целом
Интуитивное понимание случайных выборок: пример с леденцами
Малые выборки: подход пивовара
Простейшие статистические методы получения выборок
Пристрастный отбор методов выборочного обследования
Байесовская статистика
Байесовская инверсия
Раздел 4
Рекомендации по проведению опросов
Определение стоимости через готовность платить
Определение готовности к риску
Модель Раша
Определение порога вероятности на малых выборках
Есть мнение, что не все поддается количественной оценке, и невозможно просчитать все и вся. Автор книги Дуглас Хаббард развеял этот миф, и доказал всему миру, что это не так, приведя свой взгляд на оценку не измеряемого, назвав это «прикладная информационная экономика». В книге есть инструкции, таблицы, схемы, которые могут использовать все без исключения для принятия важных решений.
«Как измерить все, что угодно» очень кратко 🙂
Реальные примеры, как применять статистику и теорию вероятностей для достижения желаемых целей.
Навыки мышления в прикладном направлении могут освоить все желающие изменить свою жизнь.
Измерение: решение существует
Главная идея книги — как снизить погрешность с помощью измерений
«Вопросы Ферми»
Пример ответить на вопрос «Сколько настройщиков пианино в Чикаго»
Это скорее не измерение а оценка того что уже известно и способ приблизиться к цели
Пример 1. Какое количество настройщиков пианино в Чикаго?
Вопросы/ответы
- Численность населения Чикаго? — 3 млн (1930-1950)
- Среднее число человек в семье? — 2 или 3
- % семей пользующихся услугами настройщиков? — Макс 10%, мин 3%
- Требуемая частота настройки? — в среднем 1 раз в год
- Число пианино, настраиваемых настройщиком в день? (4 или 5 с учётом времени на дорогу)
- Количество раб дней настройщика в году? — 250
Формула:
Число настройщиков пианино в Чикаго =
(Численность населения Чикаго / на количество людей в семье х Процент семей пользующихся услугами настройщиков х Число настроек в году / (Количество пианино настраиваемых одним настройщиком за день х Число рабочих дней в году)
Ответ: В зависимости от цифр получится интервал 50-200 настройщиков (на момент когда жил Ферми — 1901-1954). Важна не столько цифра сколько ход мысли для измерения.
Пример 2. Стоит ли открывать страховой офис в Уичита-Фоллз (штат Техас)?
Вопросы/ответы
- Сколько у жителей автомобилей? — жители владели 62000 автомобилей (City-Data.com)
- Средняя годовая автомобильная страховая премия (доход страховой) в штате Техас — 837долл (Insurance Information Institute)
- Сколько машин страхуется? — почти все, потому что это требование закон-ва
- Какой размер общей выручки от страхования? — 52млн долл
- Какая средняя комиссионная ставка? — 12%
- Какой размер всего годового комиса? — 6,2 млн долл
- Сколько в городе страховых агентств? — 38 (Switchboard.com и Yellowbook.com)
- Какой размер годовой комиссии на 1 агентства? — 163тыс долл
- Рынок растёт ? — нет, население сократилось с 104 тыс до 100тыс (City-data.com на 2005 год)
- На рынке есть крупные фирмы? — да
Вывод: доходы нового агентства будут ещё меньше и это без расходов. Новое агентство лучше не открывать.
Прим. Как и с примером измерения кол-ва настройщиков пианино, важнее не конечная цифра а ход мысли при проведении измерения.
Измерение — это совокупность снижающих неопределенность наблюдений, результат которых выражается некой величиной.
Четыре предпосылки измерения
- Ваша проблема не так уникальна как вы предполагаете (возможно измерения уже проводились но в другой области)
- У вас гораздо больше информации чем вам кажется (то что важно измерить обычно оставляет следы)
- Вам нужно меньше данных чем вы предполагаете (пример — Правило Пяти)
- Существует удобный способ измерения который намного проще чем вы представляете (пример оценка улучшения качества выступления Кливлендским оркестром — вместо опросов они измеряли насколько отличалось частота бурных оваций после выступления)
Начните измерять то что вам нужно. Получив первые результаты вы всегда сможете скорректировать свой метод.
Экономическая целесообразность измерения
- Большинство переменных имеют информационную ценность близкую к нулю
- Для остальных, чья ценность велика, задайте вопрос «Существует ли вообще метод, позволяющий снизить неопределённость настолько, чтобы оправдать затраты на проведение измерения?»
Универсальный подход к измерению чего бы то ни было.
Вопросы:
- Что вы пытаетесь измерить (то есть что представляет собой объект измерения)?
- Для чего вы хотите это измерить? Какое решение будет принято после получения результатов измерения? Каким должно быть «пороговое значение» определяемого показателя?
- Какую ценность будет иметь полученная информация? К каким последствиям приведет ошибка (и какова ее вероятность)? Какие усилия по измерению будут экономически оправданы?
- Что вам уже известно? Какие интервалы или вероятности представляют собой нынешнюю неопределенность (еще до измерения)?
- Какие наблюдения позволят подтвердить или исключить те или иные возможности? Что именно мы должны увидеть сразу, если сбудется тот или иной сценарий?
- Как учесть ошибки при измерении, которых можно избежать?
Прежде чем приступить к измерениям
Формулирование задачи по измерению
Пять вопросов, которые стоит задать перед измерением:
- Какое решение будет принято с учётом результатов данного измерения?
- Что на самом деле представляет собой объект измерения?
- Почему данное измерение необходимо для принятия решения?
- Что мы знаем об объекте измерения в настоящий момент?
- Какова ценность проведения дальнейших измерений?
Неопределенность и риск
Неопределённость — существование более чем одной возможности. Истинный результат (состояние, следствие, стоимость) неизвестен
Показатель неопределенности — ряд вероятностей приписанных ряду возможностей.
Риск. Такое состояние неопределенности, когда в число возможностей нежелательные исходы (убытки, катастрофы, и тп)
Показатель риска. Набор возможностей с приписанными ими количественными вероятностями и количественно определенным ущербом.
Методы повышения качества калибровки вероятности
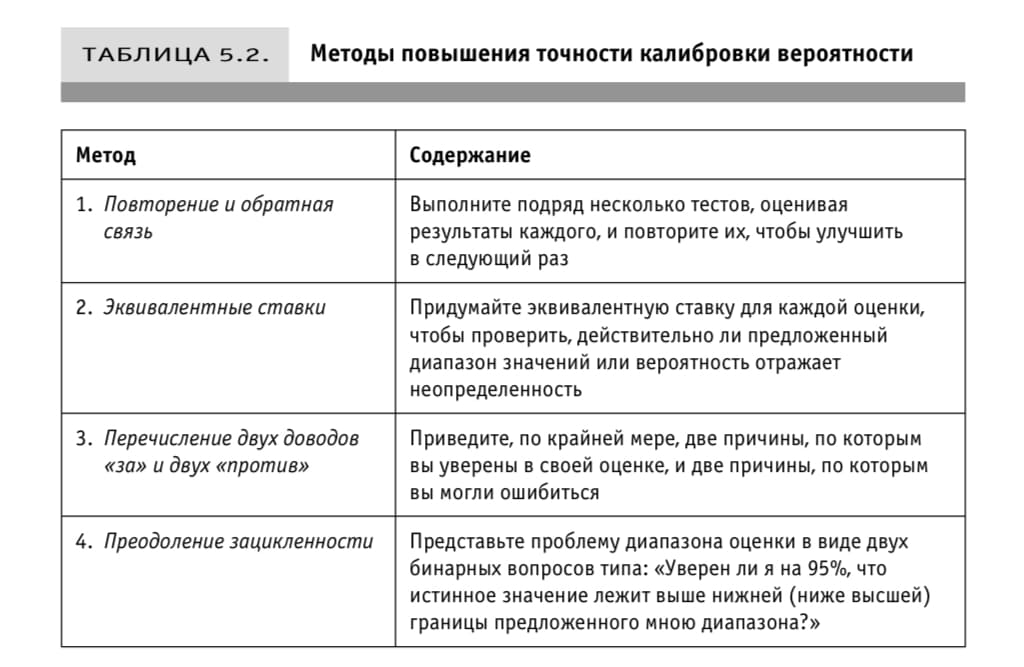
Ещё один метод — проверка на абсурдность. Задавать вопросы по верхней и нижней границе интервала пока абсурдность не исчезнет.
Хорошая статья про повышение качества калибровки.
Оценка стоимости информации
Расчёт стоимости информации помогает определить затраты на проведение ее измерений.
Речь про снижение неопределенности (шанса ошибиться).
Ошибка — когда последствия альтернативного решения оказались предпочтительнее и вы бы их выбрали.
Цена ошибки — разница между сделанными вами неправильным выбором и альтернативным лучшим вариантом из имеющихся альтернатив, который бы выбрали если бы обладали полной информацией
Потери от упущенных благоприятных возможностей (opportunity loss, OL) — это затраты которые мы понесём если выберем путь который окажется ошибочным.
Ожидаемые потери от упущенных возможностей (expected opportunity loss, EOL) — рассчитываются путём умножения вероятности допустить ошибку на цену ошибки
Простой пример:
Запуск рекламной кампании.
Калиброванный специалист даёт вероятность провала — 40%
Всего два варианта (успех/провал)
- В случае успеха компания заработает 40 млн
- В случае провала компания потеряет 5 млн долл (стоимость проведения кампании)
OL (План проведения кампании одобрен) — 5 млн долл
OL (План проведения кампании отвергнут) — 40 млн долл
EOL (План проведения кампании одобрен) — 5 млн х 40% = 2 млн долл
EOL (План проведения кампании отвергнут) — 40 млн х 60% = 24 млн долл
В этом примере, решение принимаемое без проведения измерений, заключаются в одобрении плана на проведение рекламной кампании, тогда ожидаемые потери от упущенных благоприятных возможностей составляют 2 млн долл.
Стоимость устранения любой неопределённости относительно успешности планируемой акции просто равна 2 млн долл.
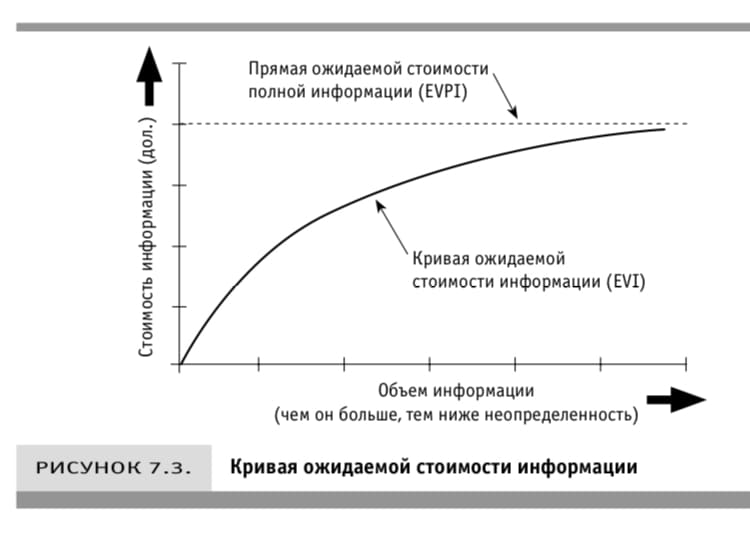
Если измерение позволяет устранить неопределённость не полностью а частично, тогда ожидаемая стоимость информации несколько сокращается.
Ожидаемая стоимость информации (EVI) = сокращение ожидаемых потерь от упущенных благоприятных возможностей
EVI = EOL (до измерений) — EOL (после измерений)
Ожидаемая стоимость полной информации (EVPI) = EOL до измерений (если информация точна и полна, то EOL после измерений равна 0)
Стоимость информации для переменных величин
«Уравнение прозрения»: стоимость информации меняет все
Если вы жаждете прозрения обратите внимание на переменную, которую прежде игнорировали
При обосновании проекта экономическая стоимость результатов измерения переменной обычно обратно пропорциональна тому, какое значение придаётся ее оценке
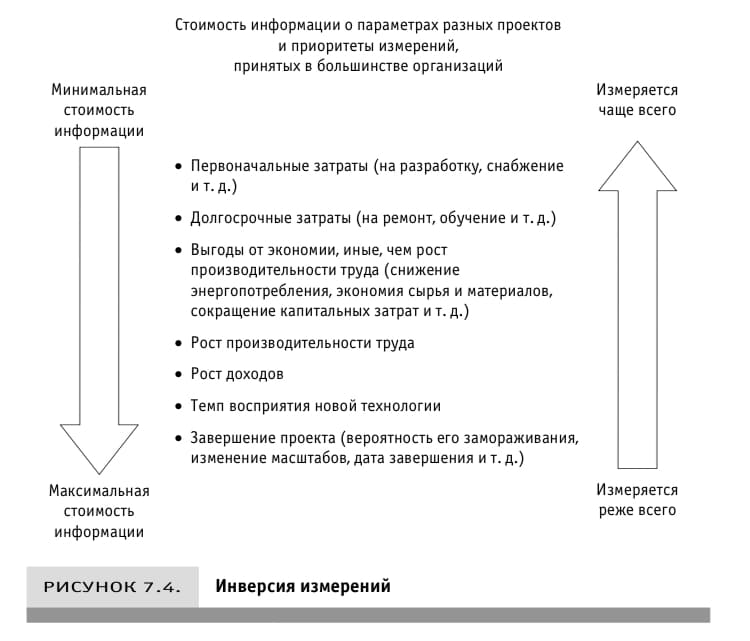
Связь между неопределённостью риском и стоимостью информации
Стоимость информации нам необходимо чтобы выбрать объект и определить какие усилия требуются для его измерения
Чему учит расчёт стоимости информации:
- Измерения процесс итеративный. Самую ценную информацию мы получаем на начальном этапе измерений, поэтому разбейте процесс на несколько этапов и подведите итоги каждого из них
- Стоимость информации имеет значение. Не определив стоимость информации вы скорее измерите не то и не так.
Методы измерения
Калькуляторы
Все калькуляторы методов собраны здесь.
Правило пяти
Существует 93-процентная вероятность что в любой случайной выборке медиана всей совокупности находится в интервале между наименьшим и наибольшим значением
- Взять 5 случайных чисел из совокупности
- Выбрать минимальное и максимальное значение
- Вероятность того, что медиана значений всей совокупности находится в интервале значений составляет 93%
Как получается 93%
- Вероятность случайного выбора значения превышающего медиану составляет 50% (как вероятность выпадения орла при подкидывании монеты)
- Вероятность случайного выбора пяти значений, которые все будут выше медианы равна вероятности выпадения орла при подкидывании монеты пять раз подряд то есть 3,125%. Такова же вероятность, что пять раз подряд все пять значений будут меньше медианы
- Тогда шанс НЕ получить все решки или все орлы составляет 100% — (3,125% х2) = 93,75%.
Метод Монте-Карло
Пояснения Монте-Карло
Статья на Википедии
Заметка с пояснениями тут
Хороший блог с пояснениями тут
Что такое стандартное отклонение тут
Калькулятор и модель тут
Прогноз расчета положительного ROI платного Slack
Возможности: позволяет, имея интервалы значений (а не точные параметры), оценить вероятность риска (например не достигнуть показателя доходности/ или получения убытка)
Пример:
Вы хотите арендовать новый станок. Стоимость годовой аренды станка 400 000 дол., и договор нужно подписать на несколько лет. Поэтому, даже не достигнув точки безубыточности, вы всё равно не сможете сразу вернуть станок. Вы собираетесь подписать договор, думая, что современное оборудование позволит сэкономить на трудозатратах и стоимости сырья и материалов, а также считаете, что материально-техническое обслуживание нового станка обойдется дешевле.
Ваши калиброванные специалисты по оценке дали следующие интервалы значений ожидаемой экономии и годового объема производства:
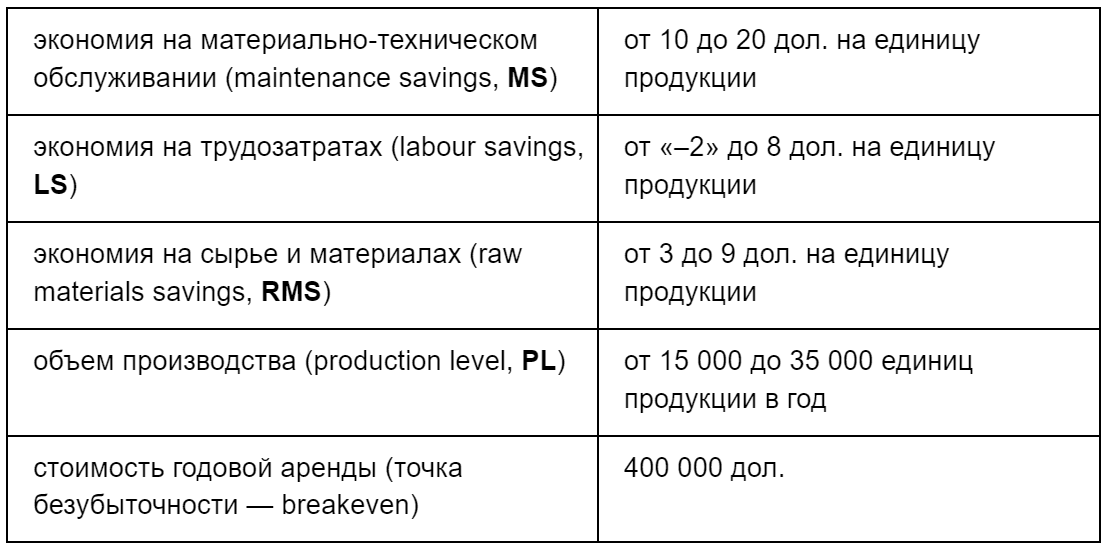
Годовая экономия составит: (MS + LS + RMS) х PL
Если мы возьмем среднее каждого из интервалов значений, то получим годовую экономию: (15 + 3 + 6) х 25 000 = 600 000 (дол.)
Один из способов взглянуть на риск – представить вероятность того, что мы не добьемся безубыточности, то есть что наша экономия окажется меньше годовой стоимости аренды станка. Чем больше нам не хватит на покрытие расходов на аренду, тем больше мы потеряем. Сумма 600 000 дол. – это медиана интервала. Как определить реальный интервал значений и рассчитать по нему вероятность того, что мы не достигнем точки безубыточности?
Моделирование методом Монте-Карло – превосходный способ решения подобных проблем. Мы должны лишь случайным образом выбрать в указанных интервалах значения, подставить их в формулу для расчета годовой экономии и рассчитать итог.
Одни результаты превысят рассчитанную нами медиану 600 000 дол., а другие окажутся ниже. Некоторые будут даже ниже требуемых для безубыточности 400 000 дол.
Кривая распределения.
Для разных величин больше подходят кривые одной формы, чем другой. В случае 90%-ного доверительного интервала обычно используется кривая нормального (гауссова) распределения. Это колоколообразная кривая, на которой большинство возможных значений результатов группируются в центральной части графика и лишь немногие, менее вероятные, распределяются, сходя на нет к его краям (рис. 1).
Вот как выглядит нормальное распределение:
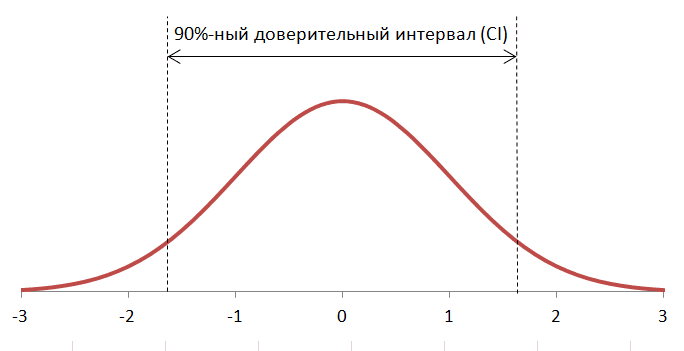
Рис.1. Нормальное распределение
Особенности:
- значения, располагающиеся в центральной части графика, более вероятны, чем значения по его краям;
- распределение симметрично; медиана находится точно посередине между верхней и нижней границами 90%-ного доверительного интервала (CI);
- «хвосты» графика бесконечны; значения за пределами 90%-ного доверительного интервала маловероятны, но все же возможны.
Стандартное отклонение.
Рисунок 1 показывает, что в одном 90%-ном доверительном интервале насчитывается 3,29 стандартного отклонения, поэтому нам просто нужно будет сделать преобразование.
В нашем случае следует создать в электронной таблице генератор случайных чисел для каждого интервала значений. Начнем, например, с MS – экономии на материально-техническом обслуживании.
Воспользуемся формулой Excel: =НОРМОБР(вероятность;среднее;стандартное_откл), где
Вероятность – вероятность, соответствующая нормальному распределению;
Среднее – среднее арифметическое распределения;
Стандартное_откл – стандартное отклонение распределения.
В нашем случае:
Среднее (медиана) = (Верхняя граница 90%-ного CI + Нижняя граница 90%-ного СI)/2;
Стандартное отклонение = (Верхняя граница 90%-ного CI – Нижняя граница 90%-ного СI)/3,29.
Примечание:
Откуда значение 3,29 —
3,29 — это расстояние по оси х от нижней до верхней границы интервала, в который попадают 90% значений случайной величины. Т.е., имеется колоколообразная кривая с математическим ожиданием μ=0. Вопрос: определите нижнюю и верхнюю границы интервала с центром в математическом ожидании, который содержит 90% значений случайной величины.
Ответ: -1,645 и + 1,645. А расстояние между границами =1,645*2 = 3,29.
Для точного вычисления можно воспользоваться формулой в Excel =НОРМ.СТ.ОБР(95%)-НОРМ.СТ.ОБР(5%). Подробнее см. заметку Нормальное распределение.
Для параметра MS формула имеет вид: =НОРМОБР(СЛЧИС();15;(20-10)/3,29), где
- СЛЧИЛ – функция, генерирующая случайные числа в диапазоне от 0 до 1;
- 15 – среднее арифметическое диапазона MS;
- (20-10)/3,29 = 3,04 – стандартное отклонение; напомню, что смысл стандартного отклонения в следующем: в интервал 3,29*Стандарт_откл, расположенный симметрично относительного среднего, попадает 90% всех значений случайной величины (в нашем случае MS)
Распределение величины экономии на материально-техническом обслуживании для 100 случайных нормально распределенных значений:
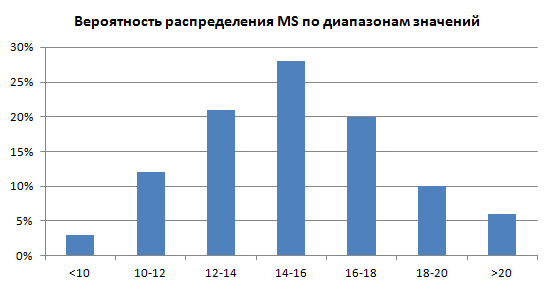
Рис. 2. Вероятность распределения MS по диапазонам значений
Поскольку мы использовали «лишь» 100 случайных значений, распределение получилось не таким уж и симметричным. Тем не менее, около 90% значений попали в диапазон экономии на MS от 10 до 20 долл. (если быть точным, то 91%).
Построим таблицу на основе доверительных интервалов параметров MS, LS, RMS и PL (рис. 3).
Два последних столбца показывают результаты расчетов на основе данных других столбцов. В столбце «Общая экономия» показана годовая экономия, рассчитанная для каждой строки. Например, в случае реализации сценария 1 общая экономия составит (14,3 + 5,8 + 4,3) х 23 471 = 570 834 долл. Столбец «Достигается ли безубыточность?» вам на самом деле не нужен. Я включил его просто для информативности. Создадим в Excel 10 000 строк-сценариев.
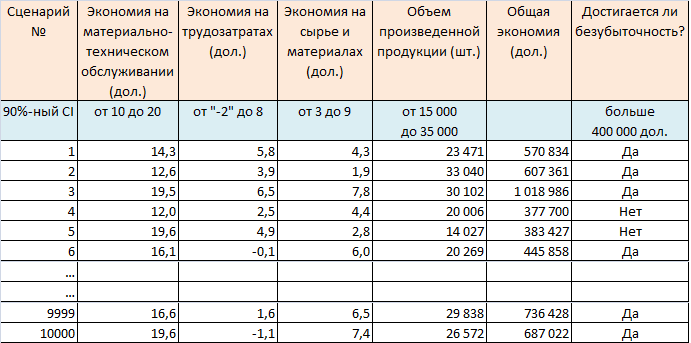
Рис. 3. Расчет сценариев методом Монте-Карло в Excel
Чтобы оценить полученные результаты, можно использовать, например, сводную таблицу, которая позволяет подсчитать число сценариев в каждом диапазоне.
Затем вы строите график, отображающий результаты расчета (рис. 4). Этот график показывает, какая доля из 10 000 сценариев будут иметь годовую экономию в том или ином интервале значений. Например, около 3% сценариев дадут годовую экономию более 1М дол.
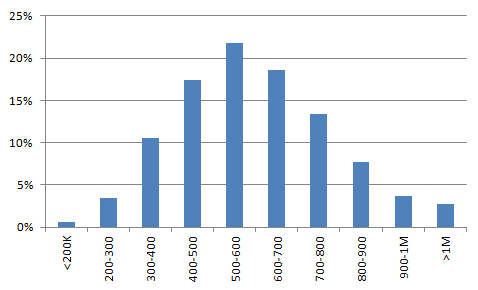
Рис. 4. Распределение общей экономии по диапазонам значений. По оси абсцисс отложены 100-тысячные диапазоны размера экономии, а по оси ординат доля сценариев, приходящихся на указанный диапазон
Из всех полученных значений годовой экономии примерно 15% будут меньше 400К дол.
Это означает, что вероятность ущерба составляет 15%. Данное число и представляет содержательную оценку риска. Но риск не всегда сводится к возможности отрицательной доходности инвестиций. Оценивая размеры вещи, мы определяем ее высоту, массу, обхват и т.д. Точно так же существуют и несколько полезных показателей риска. Дальнейший анализ показывает: есть 4%-ная вероятность того, что завод вместо экономии будет терять ежегодно по 100К дол. Однако полное отсутствие доходов практически исключено. Вот что подразумевается под анализом риска – мы должны уметь рассчитывать вероятности ущерба разного масштаба. Если вы действительно измеряете риск, то должны делать именно это.
Идеи из книги
Для чего: чтобы упростить построение прогнозных моделей разными сотрудниками компании:
- Введение в компании должности/роли — специалист по вероятностям для управления показателями вероятности
- Использовать стохастический информационные пакеты — заранее разработанный набор из 100 000 случайных значений того или иного показателя
- Использовать стохастические библиотечные модули — набор коррелирующих между собой стохастических информационных пакетов (вроде связи дохода компании с ростом экономики страны)
- Процедура сертификации калиброванных специалистов
- Документирование процедуры построения моделей начиная с исходных оценок калиброванных специалистов
Переход от объекта к способу измерения
Вопросы:
- Каковы составляющие интересующего вас объекта?
- Разложите неизвестный объект так чтобы по составляющим с собственными неопределенностями оценить целое
- Как интересующие вас объекты или его составляющие измерялись ранее?
- Анализ работы других авторов называется вторичный исследования
- В чем проявляют себя выявленные составляющие объекта измерения?
- Что на самом деле нам необходимо знать чтобы проводить измерения?
- Что может вызвать ошибку? Подумайте над тем каким образом наблюдения могут ввести заблуждение
- Какой инструмент необходимо выбрать? Возможно в этом вам также помогут вторичные исследования
Инструменты наблюдения: введение в инструментарий измерения
Приборы всегда дают погрешность. Вопрос только по сравнению с чем? Цель измерения — снижение неопределенности а не обязательное ее устранение
Разложение на составляющие: алгоритм
Многие измерения начинаются с разложения неизвестной величины на составляющие с целью выявления того что можно наблюдать непосредственно и что легче поддается количественной оценке
Алгоритм:
- Определить переменную, которая является производной от других, более простых
- Измерить более простые переменные
- Получить результат
Пример (на основе прогноза эффективности внедрения эл документооборота):
- Контекст — новый процесс электронного документооборота
- Калиброванный специалист дал очень широкий диапазон роста эффективности — 5%-40%
- Ключевая причина такой оценки — неясно количество специалистов которые будут задействованы
Вопросы:
- На какие виды деятельности документооборота сотрудники тратят больше всего времени и на какие будут намного меньше после внедрения технологии?
- Сколько времени в неделю на это уходит сейчас? Пока подойдут и калиброванные оценки
- Сколько времени удастся сэкономить?
- Зависит ли это от вида деятельности сотрудника?
- Сколько сотрудников относятся к каждой категории и сколько каждый из них тратит на подобную деятельность
Ключевое действие — найти обобщающий признак для группировки по категориям (по функциям, по продолжительности выполнения задачи)
Эффект разложения на составляющие состоит в том, что сам процесс нередко обеспечивает такое снижение неопределенности что дальнейшие наблюдения становятся ненужными
Вторичные исследования: предположим что до вас этот объект уже измеряли
Исследование начинается с анализа результатов полученных до вас.
Поиск в Интернете
- Wikipedia
- Ключевые слова в Google: таблица, опрос, корреляция, контрольная группа, стандартное отклонение; университет, доктор наук, общенациональное исследование — для поиска исследований
- Сайты бюро переписи населения США, министерства торговли, ЦРУ (World fact book)
- Поисковые машины https://www.yippy.com и https://www.yahoo.com
- Просмотр источников статьи даже если она не совсем по теме запроса
Вопросы:
- Оставляет ли объект измерения какие либо следы после себя? Найти корреляцию с другим объектом или результатом (пример: сокращение доходов от того что клиенты бросают трубку ожидая ответа поддержки)
- Понаблюдайте за составляющей объекта непосредственно (пример: выборка в определённые часы количества номеров машин из других шпатов на парковке магазина)
- Можете ли вы придумать способ «пометить» объект? (Пример: бесплатная подарочная упаковка от Amazon чтобы измерять сколько книг покупается в подарок)
Учитывайте погрешность
Ошибку не исключаемою путем усреднения называют отклонением или смещением.
Три вида отклонений при наблюдениях:
- Смещение ожидания — принятие желаемого за действительное. Люди доверчивы и склонны к самообману. Решение — испытания вслепую вроде плацебо при лечении
- Смещение выбора. Выборка которая планировалась как случайная, может оказаться неслучайной (опрос прохожих в деловом центре, на определённой улице может привести что опрошенные будут одного типа даже если были выбраны наугад)
- Ошибка наблюдателя. Влияние на объект самим фактом наблюдения. Выход — проводить наблюдения в тайне от испытуемых.
- могут ли целители бесконтактного массажа ощущать ауру пациента на расстоянии (вместо вопросов какой эффект даёт бесконтактный массаж и есть ли он вообще)
- Смогут ли клиенты заметить хоть какие-то изменения качества исследований и только потом рассчитывать стоимость ожидаемого повышения качества
- Контекст упражнения: дать 90% доверительный интервал для определения среднего веса леденца в упаковке. Указать в граммах.
- Вводная информация — 1 грамм = 1 кубический сантиментр воды.
- Например ответ от 2 до 4 грамм
- Если вы узнаете что первый случайный леденец из упаковки весит 1,4 гр. как изменится ваша оценка?
- Если вы узнаете результаты остальных 4 выбранных наугад леденцов: 1,4; 1,5; 1,6; и 1,1гр. Насколько изменится ваша оценка?
- Наконец есть результаты взвешивания ещё 3 леденцов (теперь их всего 7): 1,5; 0,9 и 1,7гр. Каким теперь будет ваш итоговый интервал?
- 1,4
- 1,4
- 1,5
- 1,6
- 1,1
- Сначала рассчитать Дисперсию выборки
А) Рассчитать средний вес отобранных леденцов (1,4+1,4+1,5+1,6+1,1)/5 = 1,4
Б) Вычесть это среднее из каждого значения выборки и возвести полученные результаты в квадрат:
(1,4-1,4)^2=0
(1,4-1,4)^2=0
(1,5-1,4)^2=0,01
(1,6-1,4)^2=0,04
(1,1-1,4)^2=0,09
В) Суммировать все квадраты и разделить на размер выборки минус единица
(0+0+0,01+0,04+0,09) / (5-1) = 0,035Вопрос:
Почему при вычислении дисперсии мы берём квадраты разницы?
Ответ:Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности к чему мы и стремились.
Вопрос:
почему нужно делить на размер выборки минус единица?
Ответ:- Когда мы имеем дело с генеральной совокупностью при вычислении дисперсии, мы делим на N (количество значений, то есть на 5 если бы было всего 5 леденцов).
- Когда мы имеем дело с выборкой (5 случайных леденцов из N леденцов на планете), при вычислении дисперсии делим на N-1 (то есть на 5-1=4)
- Найти среднеквадратическое отклонение: Разделить дисперсию выборки на ее размер и извлечь из полученного результата квадратный корень =SQRT(0.035/5) = 0,0837
- Найти в таблице упрощенных значений t-статистики значение t соответствующее размеру выборки (в нашем случае размер выборки = 5)
- Рассчитать ошибку выборки — Умножить найденное значение t-значение на значение квадратического отклонения: 2,13 х 0,0837 = 0,178 (это ошибка выборки в граммах)
- Суммировать ошибку выборки и средний размер леденца (чтобы получить верхнюю границу 90-процентного CI) и вычесть ошибку выборки из среднего веса леденца (чтобы получить нижнюю границу 90-процентного CI):
- Когда исходная неопределенность высока, для ее существенного снижения достаточно изучить несколько объектов из генеральной совокупности
- Оценки калиброванных специалистов осторожны (широкий диапазон). Чтобы их уточнить нужно провести дополнительные расчёты
- При 8 случайных объектах выборки нужно разложить значения по порядку и взять второе наименьшее и второе наибольшее значения.
- Результат: интервал значений с фактической степенью уверенности 93%.
- При 11 случайных значениях выборки — нужно взять третье наименьшее и наибольшие значения выборки.
- Результат: интервал значений с фактической степенью уверенности 93,5%.
- Словить 1000 рыб
- Пометить рыбу
- Отпустить рыбу в озеро
- После того как рыба перемешалась в озере отловить ещё 1000 рыбин
- Проверить сколько из них оказались помеченными. Если 50 рыб оказались помеченными, это значит что помечено 5% от всех имеющихся в озере рыб. Тогда вся популяция рыб в озере составляет 20000 рыб
- Определить дисперсию выборки. Доля объектов группы, численность которых мы хотим узнать умноженную на долю объектов вне группы.
Берём долю меченой рыбы (0,05), умножаем на долю не меченой рыбы (0,95) и получаем 0,0475 - Находим квадратичное отклонение.
Делим дисперсию выборки на размер выборки и извлекаем квадратный корень из суммы
=sqrt(0.0475/1000) равно 0,007 - Далее получаем нижнюю и верхнюю границу 90% CI для меченых рыб.
Для этого вычитаем и прибавляем из доли меченой рыбы (5% или 0,05) квадратичное отклонение (0,007) умноженное на 1,645 (z-значение 90 процентного CI).
Результат: 3,9%…6,13% (0,039…0,0613) - Высчитываем количество рыбы в озере
1000 / 0,039 = 25 641 рыб
1000 / 0,0613 = 16 313 рыб - Новые продукты приносили прибыль в первый год только в 30% случаях. P(FYP) = 30% (Probability of First Year Profit = 30%
- Для всех продуктов, которые приносили прибыль в 1й год, пробные продажи были удачными (удачные = достигнут порог реализации) только на 80%. P(S|FYP) = 80% («Условная» вероятность успеха тестирования сбыта при условии что производство продукта оказалось прибыльным уже в 1й год; S — означает успех; черта «|» — означает «при условии»)
- Пробные продажи были успешны в 40% случаев. P(S) = 40%
- Дать калиброванную оценку
- Изучить доп материалы
- Субъективно скорректировать свою оценку на основе новых знаний без доп расчетов
- Отбирайте самых беспристрастных оценщиков. Если вопрос влияет на бюджет отдела не привлекать к оценке руководителя отдела
- Проводите испытание вслепую. Предоставляйте специалистам информацию не раскрывая какую именно проблему они решают
- Разделяйте обязанности. Пусть одна группа оценит качественные данные. А вторая группа, не зная о каком продукте, отделе и тп идёт речь, даст конечный вывод
- Попадание — выпадение орла
- Попытка — число подбрасываний
- А шанс попадания — 50%
- Попадание — покупатель говорит «Да я ещё сюда вернусь»
- Попытка — размер выборки (например 20 случайных человек)
- Шанс попадания — 90% (предположение что 90% покупателей при опросе скажут что да, я ещё сюда вернусь)
- Вопрос должен быть максимально точным и коротким. Многословные вопросы вводят в замешательство
- Избегайте многозначных терминов. Мгнозначный термин — это слово с позитивной или негативной коннотацией. Пример — поддерживаете ли вы либеральную политику губернатора…?
- Не задавайте наводящих вопросов
- Избегайте составных вопросов. Пример: что вам больше нравится в машинах А и В: Рулевое колесо, Сиденье или приборная доска? Респондент не поймёт ответ на какой вопрос от него хотят получить. Разбейте вопрос
- Меняйте вопросы чтобы избежать установки на однообразные ответы. Пример: избегать вариант где «5» — это всегда хорошо.
- Покупка автомобиля дороже на 5000 долл, позволяет снизить риск погибнуть в автомобильной катастрофе на 20%
- Стандартный риск погибнуть в автокатастрофе = 0,5%
- Значит есть возможность снизить риск погибнуть в автокатастрофе с 0,5% до 0,1% (0.005 х 0.20 = 0,001 или 0,1%)
- Значит отказ от покупки автомобиля дороже на 5000 долл означает что человек оценивает свою жизнь в 5 млн долл ($5000/0,001 = $5 000 000)
- Рассчитать логарифм соотношения правильного и не правильного ответа на основе соотношения процента других респондентов в генеральной совокупности ответивших на этот вопрос правильно
Пример:
65% ответили правильно
35% ответили неправильно
Тогда логарифм будет =ln(0.35/(1-0.35)) = -0.619 - Рассчитать логарифм что этот человек ответит на любой другой вопрос правильно
Пример:
Респондент давал правильные ответы на предыдущие вопросы в 82% случаях
Тогда логарифм будет =ln(0.82/0.18) = 1.52 - Сложить оба логарифма и получить вероятность что данный респондент ответит правильно на этот вопрос учитывая 1) результаты ответа других респондентов на этот вопрос и 2) личные результаты этого респондента при ответе на предыдущие вопросы
=(-0.619)+1.52=0.9 - Опрос калиброванных экспертов для получения интервала экономии времени на дорогу у сотрудников.
ответ экспертов: 3-15% экономии - Определение порогового значения экономии времени при котором инвестиция в сервис имеет смысл
ответ: должно быть не меньше 7% экономии времени, иначе не интересно инвестировать в сервис - Выбор 10 случайных сотрудников и анализ затрат их времени на дорогу
выяснилось что только 1 сотрудник тратит меньше 7% своего времени на дорогу - Вопрос: какая вероятность, с учетом этой информации, что средний показатель действительно меньше 7% и инвестиции не оправданны?
- Проследовать действиям рисунка который показывает вероятность что медиана генеральной совокупности находится по одну сторону порога при условии что половина или большинство значений малой выборки — по другую сторону
- Результат: 0.6% — это вероятность что средний показатель генеральной совокупности (то есть всех сотрудников компании) меньше 7%. То есть вероятность этого очень мала.
- Выбрать сверху 10 — это число объектов (сотрудников) в выборке
- Найти в нижней части цифру 1 — это количество объектов (сотрудников) которые ниже порога.
- Найти точку пересечения кривой шага 2 и шага 1
- На вертикальной оси найти значение соответствующее точке на шаге 3. Значение 0,6%. Это и есть значение того что медиана генеральной совокупности ниже порога
Каков на самом деле тот вопрос, ответ на который может сделать дальнейшие исследования неактуальными?
Как наблюдение за частью рассказывает нам о целом
Генеральная совокупность — группа, сведения о которой необходимо получить
Полное обследование группы — изучение всех элементов группы
Выборочное исследование — любое исследование, не являющееся полным
Все что мы знаем «по опыту» — не больше чем выборка
Когда исходная неопределенность высока, даже малая выборка позволяет значительно снизить ее. И наоборот при узком интервале значений необходима бОльшая выборка.
Интуитивное понимание случайных выборок: пример с леденцами
Пример ответов в ходе упражнения:
Например ответ от 1 до 2 гр
Например ответ от 1,1 до 1,6
Например ответ: от 0,9 до 1,7гр
Вывод: с каждым новым результатом случайной выборки доверительный интервал сужается. И уже после первого взвешивания происходит его сокращение.
Малые выборки: подход пивовара
T-статистика Стьюдента (Госсета)
Возможности: позволяет на выборке до 30 значений подучить диапазон значения с заданным уровнем доверительного интервала.
История:
Уильяму Госсету, статистику и химику Guiness поручили определить какой из двух сортов ячменя даёт лучшее пиво с большим выходом. Он придумал как на небольшой выборке (меньше 30 значений) получить результат.
На примере леденцов
Вводные данные веса леденцов (в граммах):
Алгоритм:
t-значение = 2,13
Важно: при крупных выборках t-значение близко к z-значению нормального распределения и равно 1,645 (с ростом размера выборки оно не увеличивается)

Верхняя граница: 1,4 + 0,178 = 1,578
Нижняя граница: 1,4 — 0,178 = 1,322
Аналогично рассчитывается доверительный интервал и для более крупных выборок, только там t-значение равно 1,645
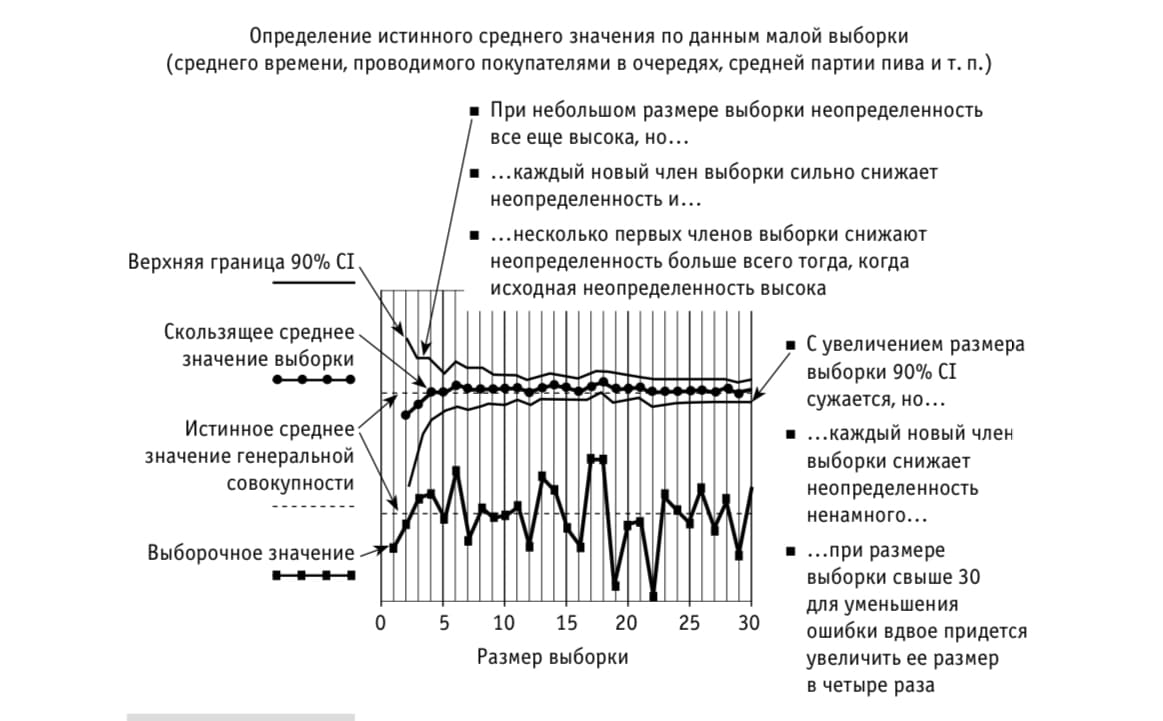
Выводы:
Простейшие статистические методы получения выборок
Более простой способ — это продолжение Правила пяти.
Фактическая степень уверенности показывает вероятность что медиана окажется в интервале значений, границами которого служат n-ное наименьшее значение и n-ное наибольшее значение выборки.
Значения представлены в таблице.
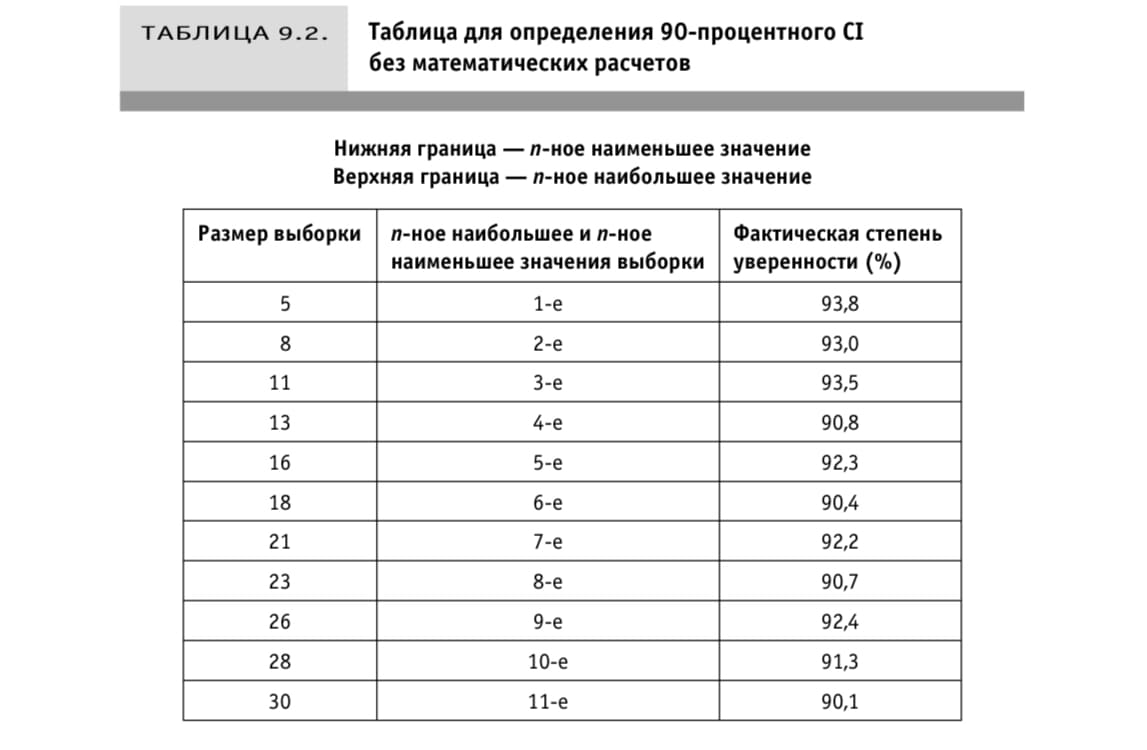
Примечание: Значения рассчитаны на основе непараметрических методов и проверены методом Монте-Карло для малых выборок.
Метод позволяет получить 90-процентный доверительный интервал лишь немного более широкий чем при использовании t-статистики. При этом проще.
Пристрастный отбор методов выборочного обследования
На примере измерения количества рыб в пруду (объема рынка/количества клиентов с которыми не сконтактировали/…)
Как измерили бы биологи количество рыбы в озере?
Как измерить размер ошибки:
Все расчёты тут
О дисперсии выборки тут
Аналогично можно считать, например, сколько клиентов не покрыто менеджерами
Вывод: если нельзя увидеть целиком какую-то группу это не означает что ее нельзя измерить
Байесовская статистика
Возможности: позволяет рассчитать вероятность результата на основе ранее проводимого наблюдения. Например вероятность успеха продаж после положительного теста спроса рынка.
Байесовская статистика занимается вопросом: как мы корректируем свое предварительное знание с учетом новой информации?
Теорема Байеса гласит, что вероятность наступления «события» при условии проведения «наблюдения» равна произведению вероятности наступления события и вероятности проведения наблюдения при условии наступления события деленному на безусловную вероятность проведения наблюдения
P(A|B) =P(A) x P(B|A)/P(B)
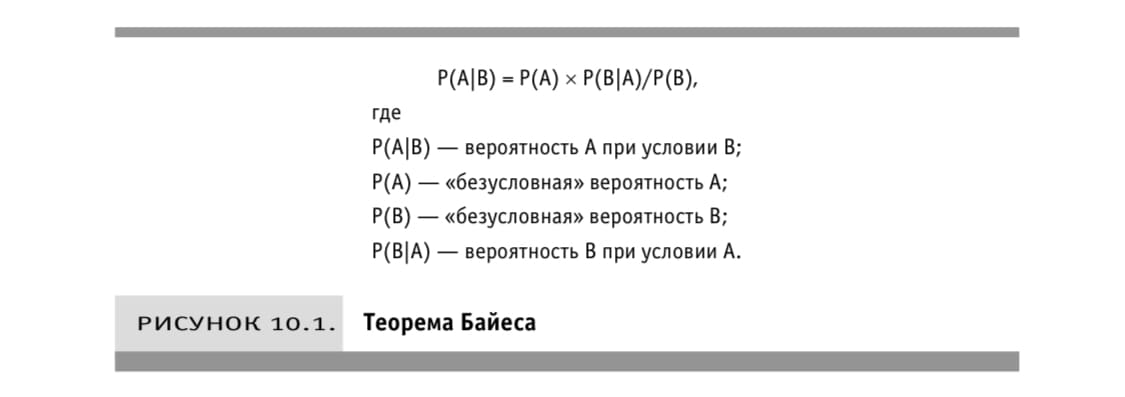
Пример:
Контекст — решается выпускать новый продукт в серийное производство или нет
Имеющиеся данные:
Вопрос:
Какая вероятность получения прибыли в 1й год при условии что тестирование сбыта окажется удачным?
Ответ:
P(FYP|S) — вероятность получения прибыли в первый же год, при условии успешного тестирования сбыта (вероятность наступления FYP при условии S)
P(FYP) — Безусловная вероятность получения прибыли в первый же год
P(S) — Безусловная вероятность успешного тестирования сбыта
P(S|FYP) — вероятность успешного тестирования сбыта при условии получения прибыли в первый же год
Вероятность получения прибыли от продукта в первый же год при условии успешного тестирования сбыта:
P(FYP|S) = P(FYP) x P(S|FYP)/P(S) = 30% x 80%/40% = 60%
Если пробный рынок показал успех, то вероятность получения прибыли в первый же год равна 60%
Вероятность получения прибыли от продукта в первый же год при условии провального тестирования сбыта:
Для всех продуктов, которые были прибыльными уже в первый год пробные продажи были успешны в 80% случаев
ЗНАЧИТ среди прибыльных в 1й год продуктов пробные продажи были провальными в 20% случаев. P(~S|FYP) = 20%
Пробные продажи были успешными в 40% случаев,
ЗНАЧИТ пробные продажи были провальными в 60% случаев. P(~S) = 60%
P(~FYP|S) = P(FYP) x P(~S|FYP)/P(~S) = 30% x 20%/60% =10%
Таким образом, провальный результат тестирования рынка даёт вероятность получения прибыли в первый же год всего 10%
Не зная вероятности получения некоего результата мы можем оценить вероятности наступления других событий и на их основе выяснить недостающие.
Пример:
Мы не знаем P(S) — вероятность успешного теста продаж.
Мы можем рассчитать эту величину на основе других значений.
Калиброванный специалист дал оценку P(S|FYP) = 80%
Также калиброванный эксперт дал оценку вероятности удачных пробных продаж продукта, который позже окажется убыточным (классический пример — “New Coke”): P(S|~FYP) = 23%
P(FYP) = 30% значит P(~FYP) = 70%
Суммируем произведение вероятности каждой вероятности на вероятность выполнения данного условия:
P(S) = P(S|FYP)xP(FYP) + P(S|~FYP)xP(~FYP)
P(S) = 80% x 30% + 23% x 70% = 40%
Алгоритм оценки с учетом новых знаний
Советы:
Байесовская инверсия
Возможности: позволяет определить вероятность конкретного результата с использованием биноминального распределения.
Биноминальное распределение позволяет рассчитать вероятность определенного числа «попаданий» при условии проведения определенного числа «попыток» и того что в каждой попытке может быть только один результат.
Пример при подбрасывание монетки.
Например мы хотим узнать какая вероятность что при 10 подбрасываниях орёл выпадет точно 4 раза при вероятности его выпадения 50%.
=binomdist(число попаданий, число попыток, вероятность попадания, 0)
=binomdist(4, 10, 0.5, 0) результат 20.5%
20.5% — это вероятность что при 10 подбрасываниях орёл выпадет ровно 4 раза.
«0» в конце означает, что нас интересует конкретный результат (4 выпадения)
Если поставить «1» тогда получим накопленную вероятность указанного или меньшего числа попаданий.
Ссылка на калькулятор тут
Ссылка на расчеты из книги тут
Пример с магазином
Вероятность конкретного результата при случайной выборке 20 покупателей что только 14 покупателей вернуться в магазин, хотя вообще таких людей должно быть 90%
=binomdist(14, 20, 0.9, 0) = результат 0.89%
Байесовская инверсия учит:
«Какова вероятность что справедливо Y если мы наблюдаем Х?»
Вместо
«Какой я должен сделать вывод из того что я вижу?»
Раздел 4
Рекомендации по проведению опросов
Систематическая ошибка — ошибка при которой ответ респондента не отвечает его истинному мнению.
Как избежать систематической ошибки:
Определение стоимости через готовность платить
WTP — willingness to pay (готовность платить)
Пример — измерение стоимости жизни человека
VSL — Value of statistical life (стоимость среднестатистической жизни). В этом случае у людей не спрашивают напрямую во сколько они оценивают свою жизнь, но просят озвучить сумму незначительного снижения риска своей преждевременной смерти
Не примере оценки стоимости жизни:
Определение готовности к риску
Современная портфельная теория (Modern Portfolio Theory — MPT)
Какая сумма инвестиций? — например 2500 долл
Точка 1. Какой макс приемлемый риск, какая мин приемлемая доходность? — например 50% ROI при риске 20% потери. Эта точка лежит на инвестиционной границе.
Точка 2. Какой макс риск должен быть чтобы такая доходность оказалась неприемлемой?
Точка 3. Какая мин доходность приемлема при отсутствии риска? — например 10%
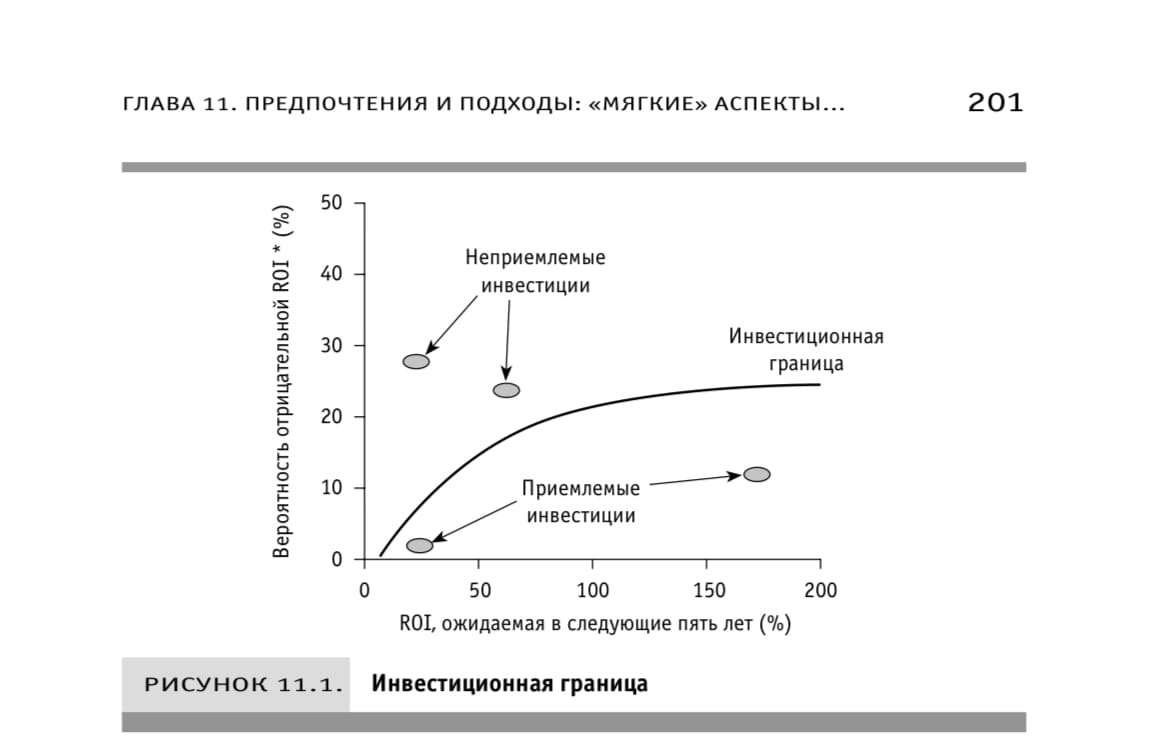
Главное правило измерения — никогда не используйте метод способный увеличить ошибку первоначальной оценки.
Модель Раша
Возможности: позволяет предсказать вероятность что испытуемый ответит правильно на вопросы теста на основе 1) процента других респондентов в генеральной совокупности ответивших на этот вопрос правильно и 2) процента других вопросов на которые данный испытуемый уже ответил правильно
Алгоритм:
Тогда логарифм будет =1/(1/exp(0.9)+1)=0.71
Это означает вероятность 71% что данный респондент ответит правильно на этот вопрос учитывая 1) результаты ответа других респондентов на этот вопрос и 2) личные результаты этого респондента при ответе на предыдущие вопросы
Определение порога вероятности на малых выборках
Возможности: позволяет измерить вероятность того что среднее значение совокупности будет ниже порога.
Контекст (пример):
Расчёт целесообразности оплаты сервиса для проведения совещаний сотрудников дистанционно. Гипотеза что если на совещаниях обсуждаются рутинные вопросы, то экономия времени на дорогу позволит окупить затраты на сервис онлайн совещаний.
Алгоритм:
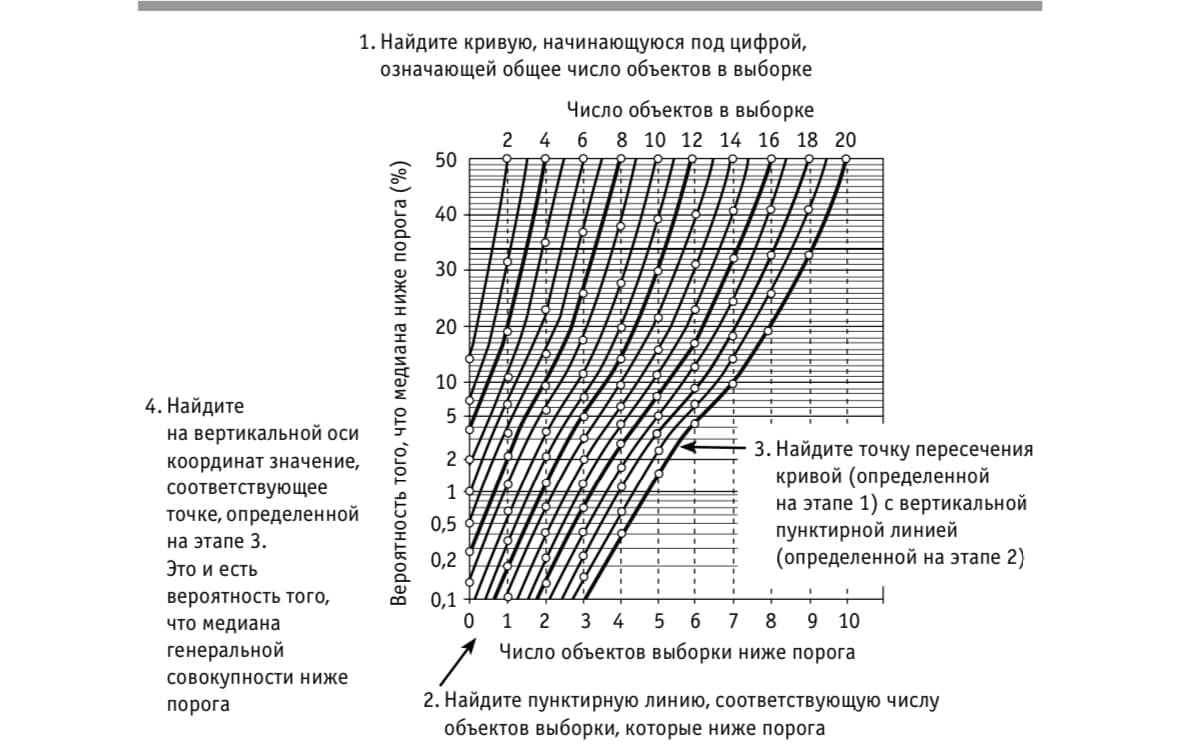
Пояснение:
Похожие книги
📝 Отзывы о книге Дугласа Хаббарда «Как измерить все что угодно»
Не сдерживайте себя и с помощью формы комментариев чуть ниже расскажите все, что вам понравилось или не понравилось в книге. Советуете почитать? Или может держаться от нее подальше? 🙂